Workflow overview

Models in R can generally be fit using a formula interface. The fitted models can then be explored and post-processed in various was, for example to display an ANOVA-style table, calculate confidence intervals, or plot predictions from the model. This package provides additional post-estimation functions to calculate expected values along with simulation-based estimates of uncertainty.

Examples

Let’s walk through an example. This example uses the Prestige dataset. It contains data on 102 occupations. We will model the effect of education and type on income.

Building Models

Since income is a continuous variable, least squares is an appropriate model choice. To estimate our model, we call the lm function:

# load data
options(StringsAsFactors = FALSE)
data(Prestige, package = "car")

Prestige <- na.omit(Prestige)

# estimate ls model
m1 <- lm(income ~ education + type, data = Prestige)

# model summary
summary(m1)

## 
## Call:
## lm(formula = income ~ education + type, data = Prestige)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6242.7 -1768.0  -408.3  1149.1 16939.3 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)  -2048.2     2431.5  -0.842  0.40171   
## education      887.9      284.7   3.119  0.00241 **
## typeprof       102.1     1805.3   0.057  0.95501   
## typewc       -2685.8     1140.5  -2.355  0.02061 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3312 on 94 degrees of freedom
## Multiple R-squared:  0.4052, Adjusted R-squared:  0.3862 
## F-statistic: 21.35 on 3 and 94 DF,  p-value: 1.249e-10

Since this is an ordinary least squares regression, the coefficients are themselves quantities of interest. The education coefficient tells us that (holding occupation type constant) every additional year of education is associated with an $887.9 increase in income. The coefficients for typeprof and typewc are slightly more difficult to interpret. They are dummy codes that tell us the expected difference between blue-collar and professional incomes, and between blue-collar and white-collar incomes.

Although the model coefficients are not difficult to interpret, expected values are even more straight-forward. We can calculate them using the smargins function.

library(smargins)

ppred1 <- smargins(m1, type = unique(type))

ppred1

##       type .sim_number .smargin_qi
## 1     prof           1    7924.766
## 2     prof           2    8185.379
## 3     prof           3    6451.597
## 4     prof           4    7425.381
## 5     prof           5    7411.770
## 6     prof           6    6695.249
## # - - - - - - - - - - - - - - - - -                                  
## 14995   wc        4995    4050.739
## 14996   wc        4996    6131.891
## 14997   wc        4997    4503.442
## 14998   wc        4998    3597.820
## 14999   wc        4999    5699.268
## 15000   wc        5000    5169.789

The print method shows us how the result is organized. There is a summary method that gives a default set of statistics for each combination of values specified in the at argument:

summary(ppred1)

##   type     mean        sd   median lower_2.5 upper_97.5
## 1 prof 7639.212 1112.5612 7624.771  5471.654   9834.930
## 2   bc 7542.398  847.4511 7547.717  5821.903   9153.423
## 3   wc 4840.311  700.2960 4828.906  3483.344   6218.822

Comparisons

The summary method shows expected values for each value specified in the ... arguments, but frequently we want some transformation of these values. There is a scompare function that gives pairwise differences:

summary(scompare(ppred1, "type"))

##         type       mean       sd     median  lower_2.5 upper_97.5
## 1 prof vs bc 2798.90120 1266.006 2785.93852   380.9055   5290.244
## 2 prof vs wc  -96.81424 1797.696  -82.22986 -3648.5200   3429.564
## 3   bc vs wc 2702.08696 1149.508 2717.07318   462.2639   4888.239

but the really great thing is that the structure is simple enough that the user can perform their own arbitrary transformations. For example, we can compare the average of white collar and professional with blue collar:

bc <- subset(ppred1, type == "bc")$.smargin_qi
wc_prof <- subset(ppred1, type == "wc")$.smargin_qi +
           subset(ppred1, type == "wc")$.smargin_qi
sumstats(bc - wc_prof)

##       mean         sd     median  lower_2.5 upper_97.5 
##  -2041.410   1717.267  -2063.545  -5284.473   1258.301

Visualizations

Another advantage of the simple data structure returned by smargins is that it makes creating plots using standard graphics packages in R easy. For example, we can graph the expected values by type:

library(ggplot2)

ggplot(summary(ppred1),
       aes(x = mean, y = type)) +
    geom_point() +
    geom_errorbarh(aes(xmin = lower_2.5, xmax = upper_97.5),
                   height = 0.25)

ggplot(ppred1,
       aes(x = .smargin_qi)) +
    geom_density(aes(fill = type), alpha = 0.25)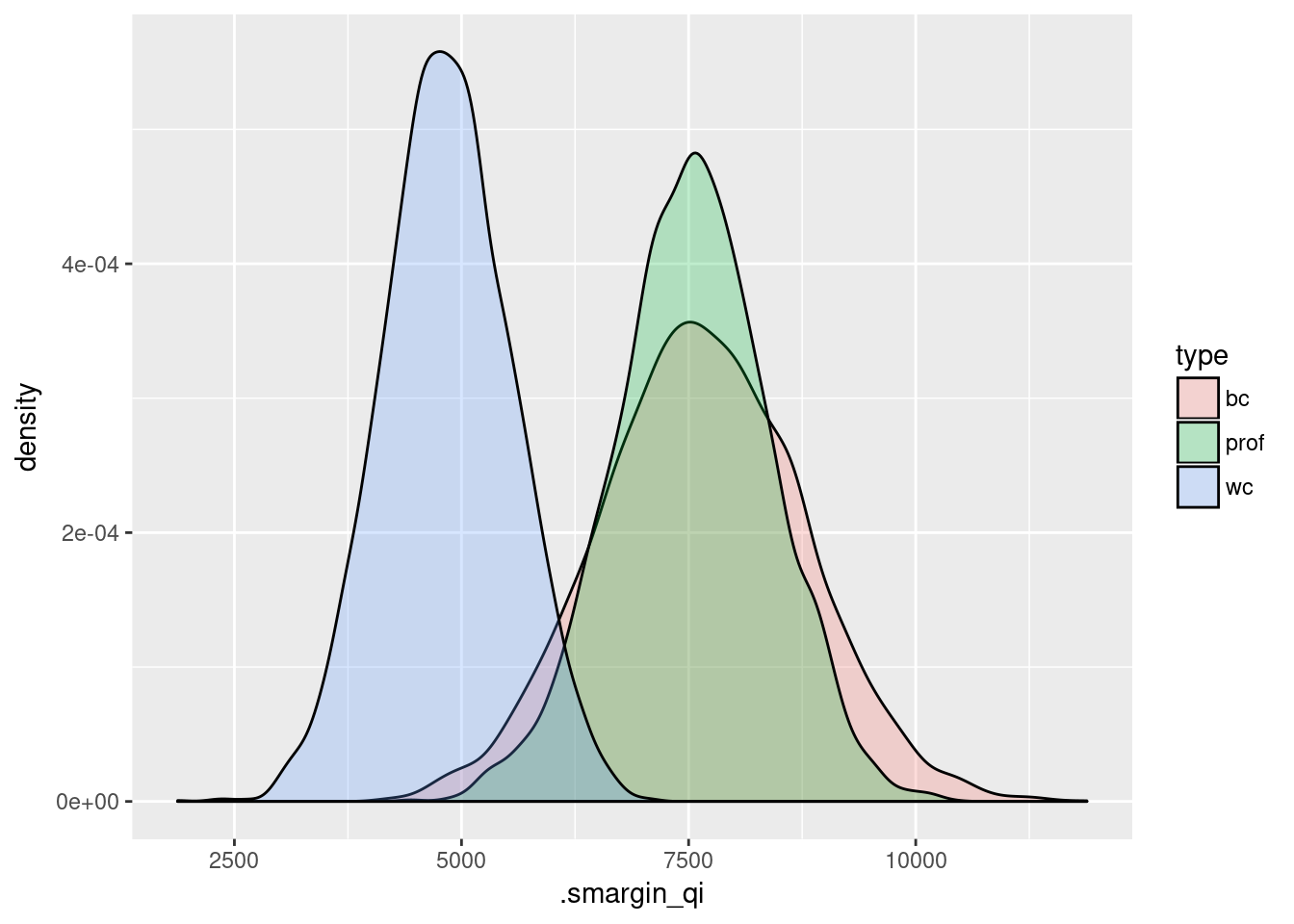

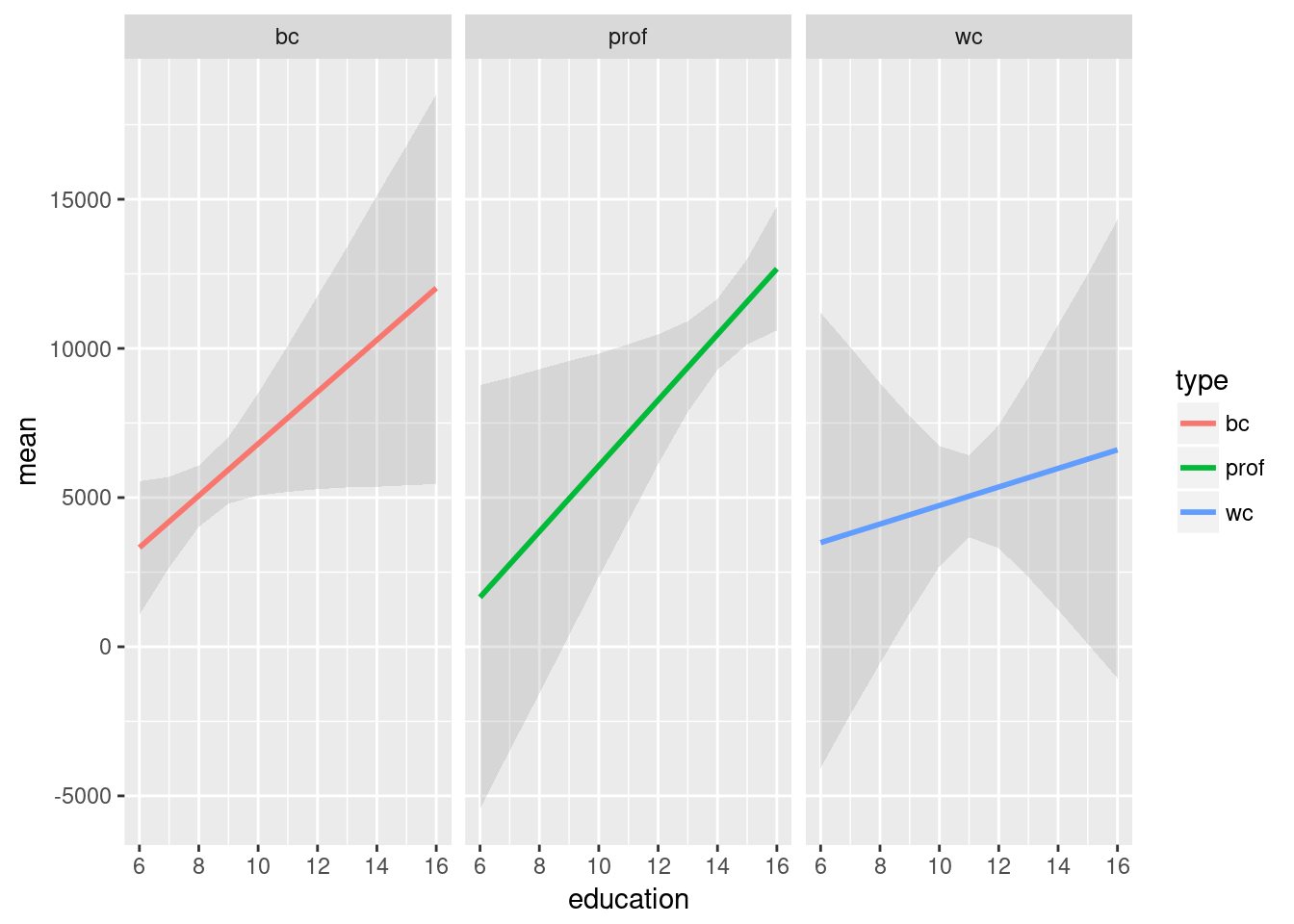
This is especially useful for plotting interactions:

m2 <- lm(income ~ education*type, data = Prestige)

m2.sm <- smargins(m2, education = 6:16, type = c("bc", "prof", "wc"))

ggplot(summary(m2.sm),
       aes(x = education, y = mean, color = type)) +
    geom_smooth(aes(ymin = lower_2.5, ymax = upper_97.5),
                stat = "identity",
                alpha = 0.25) + facet_wrap(~type)

## Warning: Ignoring unknown aesthetics: ymin, ymax