R Regression Models
Topics
- Formula interface for model specification
- Function methods for extracting quantities of interest from models
- Contrasts to test specific hypotheses
- Model comparisons
- Predicted marginal effects
Setup
Class Structure
- Informal — Ask questions at any time. Really!
- Collaboration is encouraged - please spend a minute introducing yourself to your neighbors!
Prerequisites
This is an intermediate R course:
- Assumes working knowledge of R
- Relatively fast-paced
- This is not a statistics course! We will teach you how to fit models in R, but we assume you know the theory behind the models.
Goals
We will learn about the R modeling ecosystem by fitting a variety of statistical models to different datasets. In particular, our goals are to learn about:
- Modeling workflow
- Visualizing and summarizing data before modeling
- Modeling continuous outcomes
- Modeling binary outcomes
- Modeling clustered data
We will not spend much time interpreting the models we fit, since this is not a statistics workshop. But, we will walk you through how model results are organized and orientate you to where you can find typical quantities of interest.
Launch an R session
Start RStudio and create a new project:
- On Windows click the start button and search for RStudio. On Mac RStudio will be in your applications folder.
- In Rstudio go to
File -> New Project. - Choose
Existing Directoryand browse to the workshop materials directory on your desktop. - Choose
File -> Open Fileand select the file with the word “BLANK” in the name.
Packages
You should have already installed the tidyverse and rmarkdown packages onto your computer before the workshop — see R Installation. Now let’s load these packages into the search path of our R session.
library(tidyverse)
library(rmarkdown)Finally, lets install some packages that will help with modeling:
# install.packages("lme4")
library(lme4) # for mixed models
# install.packages("emmeans")
library(emmeans) # for marginal effects
# install.packages("effects")
library(effects) # for predicted marginal meansModeling workflow
Before we delve into the details of how to fit models in R, it’s worth taking a step back and thinking more broadly about the components of the modeling process. These can roughly be divided into 3 stages:
- Pre-estimation
- Estimation
- Post-estimaton
At each stage, the goal is to complete a different task (e.g., to clean data, fit a model, test a hypothesis), but the process is sequential — we move through the stages in order (though often many times in one project!)
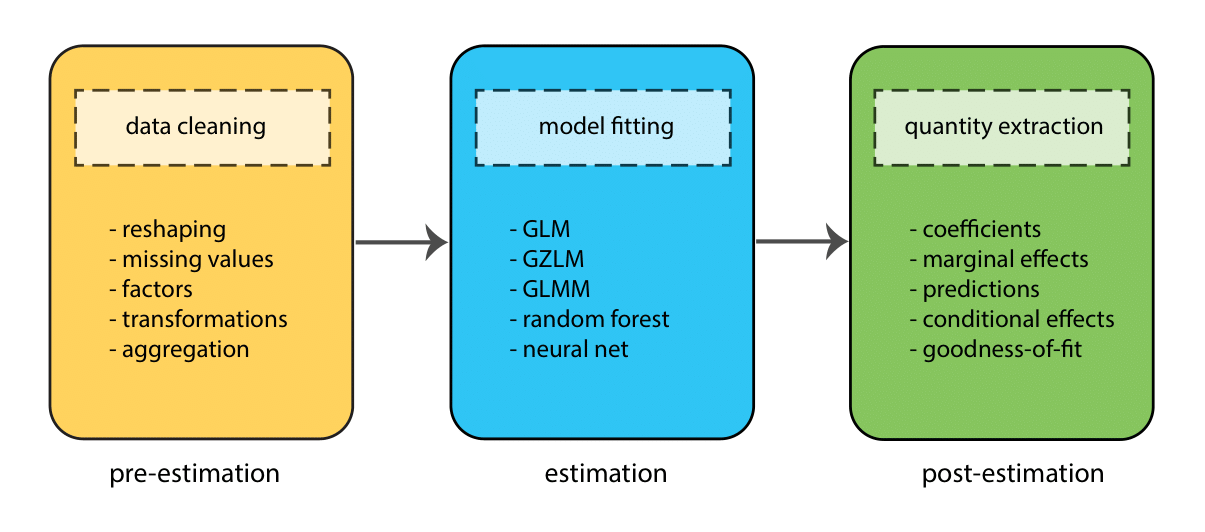
Throughout this workshop we will go through these stages several times as we fit different types of model.
R modeling ecosystem
There are literally hundreds of R packages that provide model fitting functionality. We’re going to focus on just two during this workshop — stats, from Base R, and lme4. It’s a good idea to look at CRAN Task Views when trying to find a modeling package for your needs, as they provide an extensive curated list. But, here’s a more digestable table showing some of the most popular packages for particular types of model.
| Models | Packages |
|---|---|
| Generalized linear | stats, biglm, MASS, robustbase |
| Mixed effects | lme4, nlme, glmmTMB, MASS |
| Econometric | pglm, VGAM, pscl, survival |
| Bayesian | brms, blme, MCMCglmm, rstan |
| Machine learning | mlr, caret, h2o, tensorflow |
Before fitting a model
GOAL: To learn about the data by creating summaries and visualizations.
One important part of the pre-estimation stage of model fitting, is gaining an understanding of the data we wish to model by creating plots and summaries. Let’s do this now.
Load the data
List the data files we’re going to work with:
list.files("dataSets")## [1] "Exam.rds" "NatHealth2008MI" "NatHealth2011.rds" "states.rds"We’re going to use the states data first, which originally appeared in Statistics with Stata by Lawrence C. Hamilton.
# read the states data
states_data <- read_rds("dataSets/states.rds")
# look at the last few rows
tail(states_data)## state region pop area density metro waste energy miles toxic green house senate csat vsat msat percent expense income high college
## 46 Vermont N. East 563000 9249 60.87 23.4 0.69 232 10.4 1.81 15.17 85 94 890 424 466 68 6738 34.717 80.8 24.3
## 47 Virginia South 6187000 39598 156.25 72.5 1.45 306 9.7 12.87 18.72 33 54 890 424 466 60 4836 38.838 75.2 24.5
## 48 Washington West 4867000 66582 73.10 81.7 1.05 389 9.2 8.51 16.51 52 64 913 433 480 49 5000 36.338 83.8 22.9
## 49 West Virginia South 1793000 24087 74.44 36.4 0.95 415 8.6 21.30 51.14 48 57 926 441 485 17 4911 24.233 66.0 12.3
## [ reached 'max' / getOption("max.print") -- omitted 2 rows ]| Variable | Description |
|---|---|
| csat | Mean composite SAT score |
| expense | Per pupil expenditures |
| percent | % HS graduates taking SAT |
| income | Median household income, $1,000 |
| region | Geographic region: West, N. East, South, Midwest |
| house | House ’91 environ. voting, % |
| senate | Senate ’91 environ. voting, % |
| energy | Per capita energy consumed, Btu |
| metro | Metropolitan area population, % |
| waste | Per capita solid waste, tons |
Examine the data
Start by examining the data to check for problems.
# summary of expense and csat columns, all rows
sts_ex_sat <-
states_data %>%
select(expense, csat)
summary(sts_ex_sat)## expense csat
## Min. :2960 Min. : 832
## 1st Qu.:4352 1st Qu.: 888
## Median :5000 Median : 926
## Mean :5236 Mean : 944
## 3rd Qu.:5794 3rd Qu.: 997
## Max. :9259 Max. :1093 # correlation between expense and csat
cor(sts_ex_sat, use = "pairwise") ## expense csat
## expense 1.000000 -0.466298
## csat -0.466298 1.000000Plot the data
Plot the data to look for multivariate outliers, non-linear relationships etc.
# scatter plot of expense vs csat
plot(sts_ex_sat)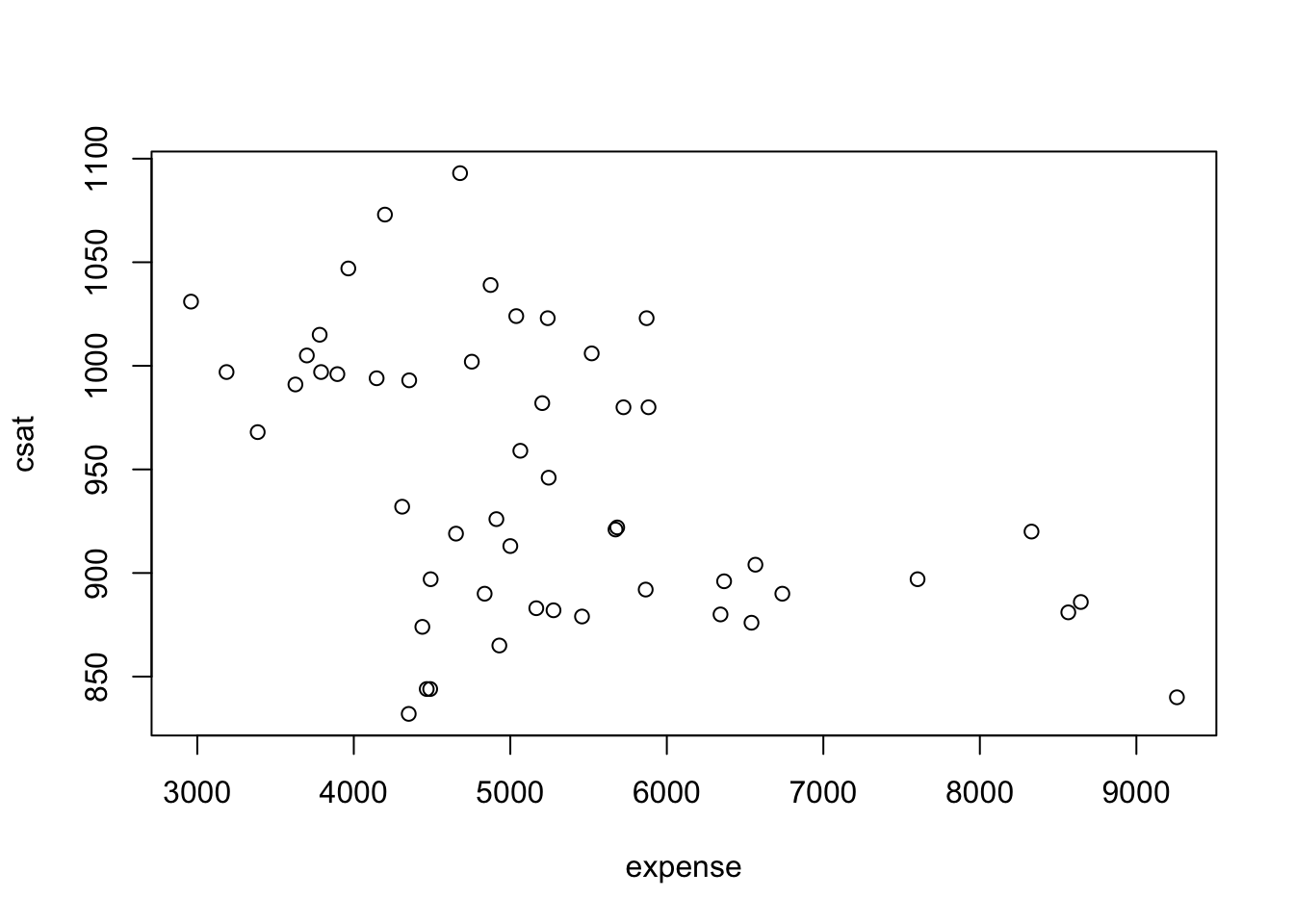
Obviously, in a real project, you would want to spend more time investigating the data, but we’ll now move on to modeling.
Models with continuous outcomes
GOAL: To learn about the R modeling ecosystem by fitting ordinary least squares (OLS) models. In particular:
- Formula representation of a model specification
- Model classes
- Function methods
- Model comparison
Once the data have been inspected and cleaned, we can start estimating models. The simplest models (but those with the most assumptions) are those for continuous and unbounded outcomes. Typically, for these outcomes, we’d use a model estimated using Ordinary Least Lquares (OLS), which in R can be fit with the lm() (linear model) function.
To fit a model in R, we first have to convert our theoretical model into a formula — a symbolic representation of the model in R syntax:
# formula for model specification
outcome ~ pred1 + pred2 + pred3
# NOTE the ~ is a tildeFor example, the following model predicts SAT scores based on per-pupil expenditures:
\[ csat_i = \beta_{0}1 + \beta_1expense_i + \epsilon_i \]
We can use lm() to fit this model:
# fit our regression model
sat_mod <- lm(csat ~ 1 + expense, # regression formula
data = states_data) # data
# look at the basic printed output
sat_mod##
## Call:
## lm(formula = csat ~ 1 + expense, data = states_data)
##
## Coefficients:
## (Intercept) expense
## 1060.7324 -0.0223 # get more informative summary information
# about coefficients and goodness-of-fit
summary(sat_mod)##
## Call:
## lm(formula = csat ~ 1 + expense, data = states_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -131.81 -38.08 5.61 37.85 136.50
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1060.73244 32.70090 32.44 < 2e-16
## expense -0.02228 0.00604 -3.69 0.00056
##
## Residual standard error: 59.8 on 49 degrees of freedom
## Multiple R-squared: 0.217, Adjusted R-squared: 0.201
## F-statistic: 13.6 on 1 and 49 DF, p-value: 0.000563 # show only the regression coefficients table
summary(sat_mod) %>% coef() ## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1060.7324439 32.70089674 32.43741 8.87841e-35
## expense -0.0222756 0.00603711 -3.68978 5.63090e-04Why is the association between expense & SAT scores negative?
Many people find it surprising that the per-capita expenditure on students is negatively related to SAT scores. The beauty of multiple regression is that we can try to pull these apart. What would the association between expense and SAT scores be if there were no difference among the states in the percentage of students taking the SAT?
lm(csat ~ 1 + expense + percent, data = states_data) %>%
summary() ##
## Call:
## lm(formula = csat ~ 1 + expense + percent, data = states_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -62.92 -24.32 1.74 15.50 75.62
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 989.8074 18.3958 53.81 < 2e-16
## expense 0.0086 0.0042 2.05 0.046
## percent -2.5377 0.2249 -11.28 0.0000000000000042
##
## Residual standard error: 31.6 on 48 degrees of freedom
## Multiple R-squared: 0.786, Adjusted R-squared: 0.777
## F-statistic: 88 on 2 and 48 DF, p-value: <2e-16The lm class & methods
Okay, we fitted our model. Now what? Typically, the main goal in the post-estimation stage of analysis is to extract quantities of interest from our fitted model. These quantities could be things like:
- Testing whether one group is different on average from another group
- Generating average response values from the model for interesting combinations of predictor values
- Calculating interval estimates for particular coefficients
But before we can do any of that, we need to know more about what a fitted model actually is, what information it contains, and how we can extract from it information that we want to report.
Let’s start by examining the model object:
class(sat_mod)## [1] "lm" str(sat_mod)## List of 12
## $ coefficients : Named num [1:2] 1060.7324 -0.0223
## ..- attr(*, "names")= chr [1:2] "(Intercept)" "expense"
## $ residuals : Named num [1:51] 11.1 44.8 -32.7 26.7 -63.7 ...
## ..- attr(*, "names")= chr [1:51] "1" "2" "3" "4" ...
## $ effects : Named num [1:51] -6742.2 220.7 -31.7 29.7 -63.2 ...
## ..- attr(*, "names")= chr [1:51] "(Intercept)" "expense" "" "" ...
## $ rank : int 2
## $ fitted.values: Named num [1:51] 980 875 965 978 961 ...
## ..- attr(*, "names")= chr [1:51] "1" "2" "3" "4" ...
## $ assign : int [1:2] 0 1
## $ qr :List of 5
## ..$ qr : num [1:51, 1:2] -7.14 0.14 0.14 0.14 0.14 ...
## .. ..- attr(*, "dimnames")=List of 2
## .. .. ..$ : chr [1:51] "1" "2" "3" "4" ...
## .. .. ..$ : chr [1:2] "(Intercept)" "expense"
## .. ..- attr(*, "assign")= int [1:2] 0 1
## ..$ qraux: num [1:2] 1.14 1.33
## ..$ pivot: int [1:2] 1 2
## ..$ tol : num 0.0000001
## ..$ rank : int 2
## ..- attr(*, "class")= chr "qr"
## $ df.residual : int 49
## $ xlevels : Named list()
## $ call : language lm(formula = csat ~ 1 + expense, data = states_data)
## $ terms :Classes 'terms', 'formula' language csat ~ 1 + expense
## .. ..- attr(*, "variables")= language list(csat, expense)
## .. ..- attr(*, "factors")= int [1:2, 1] 0 1
## .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. ..$ : chr [1:2] "csat" "expense"
## .. .. .. ..$ : chr "expense"
## .. ..- attr(*, "term.labels")= chr "expense"
## .. ..- attr(*, "order")= int 1
## .. ..- attr(*, "intercept")= int 1
## .. ..- attr(*, "response")= int 1
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. ..- attr(*, "predvars")= language list(csat, expense)
## .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
## .. .. ..- attr(*, "names")= chr [1:2] "csat" "expense"
## $ model :'data.frame': 51 obs. of 2 variables:
## ..$ csat : int [1:51] 991 920 932 1005 897 959 897 892 840 882 ...
## ..$ expense: int [1:51] 3627 8330 4309 3700 4491 5064 7602 5865 9259 5276 ...
## ..- attr(*, "terms")=Classes 'terms', 'formula' language csat ~ 1 + expense
## .. .. ..- attr(*, "variables")= language list(csat, expense)
## .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
## .. .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. .. ..$ : chr [1:2] "csat" "expense"
## .. .. .. .. ..$ : chr "expense"
## .. .. ..- attr(*, "term.labels")= chr "expense"
## .. .. ..- attr(*, "order")= int 1
## .. .. ..- attr(*, "intercept")= int 1
## .. .. ..- attr(*, "response")= int 1
## .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. .. ..- attr(*, "predvars")= language list(csat, expense)
## .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
## .. .. .. ..- attr(*, "names")= chr [1:2] "csat" "expense"
## - attr(*, "class")= chr "lm" names(sat_mod)## [1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr" "df.residual" "xlevels" "call" "terms" "model"We can list all the functions that extract particular quantities of interest (called extractor functions) by using the methods() function with the class argument set to the class of the model object:
methods(class = class(sat_mod))## [1] add1 addterm alias anova boxcox case.names coerce confint cooks.distance deviance dfbeta dfbetas drop1 dropterm
## [15] dummy.coef Effect effects emm_basis extractAIC family formula fortify hatvalues influence initialize kappa labels logLik
## [29] logtrans model.frame model.matrix nobs plot predict print proj qqnorm qr recover_data residuals rstandard rstudent
## [43] show simulate slotsFromS3 summary variable.names vcov
## see '?methods' for accessing help and source codeWe can also use function methods to get more information about the fit:
summary(sat_mod) # summary table##
## Call:
## lm(formula = csat ~ 1 + expense, data = states_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -131.81 -38.08 5.61 37.85 136.50
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1060.73244 32.70090 32.44 < 2e-16
## expense -0.02228 0.00604 -3.69 0.00056
##
## Residual standard error: 59.8 on 49 degrees of freedom
## Multiple R-squared: 0.217, Adjusted R-squared: 0.201
## F-statistic: 13.6 on 1 and 49 DF, p-value: 0.000563 confint(sat_mod) # confidence intervals## 2.5 % 97.5 %
## (Intercept) 995.0175316 1126.4473563
## expense -0.0344077 -0.0101436 anova(sat_mod) # ANOVA table ## Analysis of Variance Table
##
## Response: csat
## Df Sum Sq Mean Sq F value Pr(>F)
## expense 1 48708 48708 13.62 0.000563
## Residuals 49 175306 3578How does R know which method to call for a given object? R uses generic functions, which provide access to methods. Method dispatch takes place based on the class of the first argument to the generic function. For example, for the generic function summary() and an object of class lm, the method dispatched will be summary.lm(). Function methods always take the form generic.method():
methods("summary")## [1] summary,ANY-method summary,DBIObject-method summary,diagonalMatrix-method summary,sparseMatrix-method summary.aareg* summary.allFit*
## [7] summary.aov summary.aovlist* summary.aspell* summary.cch* summary.check_packages_in_dir* summary.connection
## [13] summary.corAR1* summary.corARMA* summary.corCAR1* summary.corCompSymm* summary.corExp* summary.corGaus*
## [19] summary.corIdent* summary.corLin* summary.corNatural* summary.corRatio* summary.corSpher* summary.corStruct*
## [25] summary.corSymm* summary.coxph* summary.coxph.penal* summary.data.frame summary.Date summary.DBIrepdesign*
## [31] summary.DBIsvydesign* summary.default summary.Duration* summary.ecdf* summary.eff* summary.efflatent*
## [37] summary.efflist* summary.effpoly* summary.emm_list* summary.emmGrid* summary.factor summary.ggplot*
## [43] summary.glht* summary.glht_list* summary.glm summary.gls* summary.hcl_palettes* summary.infl*
## [49] summary.Interval* summary.lm summary.lme* summary.lmList* summary.lmList4* summary.loess*
## [55] summary.loglm* summary.manova summary.matrix summary.mcmc* summary.mcmc.list* summary.merMod*
## [61] summary.MIresult* summary.mlm* summary.mlm.efflist* summary.modelStruct* summary.multinom* summary.negbin*
## [67] summary.nls* summary.nlsList* summary.nnet* summary.packageStatus* summary.pdBlocked* summary.pdCompSymm*
## [73] summary.pdDiag* summary.pdIdent* summary.pdLogChol* summary.pdMat* summary.pdNatural* summary.pdSymm*
## [79] summary.Period* summary.polr* summary.POSIXct summary.POSIXlt summary.ppr* summary.pps*
## [85] summary.prcomp* summary.prcomplist* summary.predictorefflist* summary.princomp* summary.proc_time summary.pyears*
## [91] summary.ratetable* summary.reStruct* summary.rlang_error* summary.rlang_trace* summary.rlm* summary.shingle*
## [97] summary.srcfile summary.srcref summary.stepfun summary.stl*
## [ reached getOption("max.print") -- omitted 35 entries ]
## see '?methods' for accessing help and source code
It’s always worth examining whether the class of model you’re fitting has a method for a particular extractor function. Here’s a summary table of some of the most often used extractor functions, which have methods for a wide range of model classes. These are post-estimation tools you will want in your toolbox:
| Function | Package | Output |
|---|---|---|
summary() |
stats base R |
standard errors, test statistics, p-values, GOF stats |
confint() |
stats base R |
confidence intervals |
anova() |
stats base R |
anova table (one model), model comparison (> one model) |
coef() |
stats base R |
point estimates |
drop1() |
stats base R |
model comparison |
predict() |
stats base R |
predicted response values |
fitted() |
stats base R |
predicted response values (for observed data) |
residuals() |
stats base R |
residuals |
fixef() |
lme4 |
fixed effect point estimates (mixed models only) |
ranef() |
lme4 |
random effect point estimates (mixed models only) |
coef() |
lme4 |
empirical Bayes estimates (mixed models only) |
allEffects() |
effects |
predicted marginal means |
emmeans() |
emmeans |
predicted marginal means & marginal effects |
margins() |
margins |
predicted marginal means & marginal effects |
OLS regression assumptions
OLS regression relies on several assumptions, including:
- The model includes all relevant variables (i.e., no omitted variable bias).
- The model is linear in the parameters (i.e., the coefficients and error term).
- The error term has an expected value of zero.
- All right-hand-side variables are uncorrelated with the error term.
- No right-hand-side variables are a perfect linear function of other RHS variables.
- Observations of the error term are uncorrelated with each other.
- The error term has constant variance (i.e., homoscedasticity).
- (Optional - only needed for inference). The error term is normally distributed.
Investigate assumptions #7 and #8 visually by plotting your model:
par(mfrow = c(2, 2)) # splits the plotting window into 4 panels
plot(sat_mod)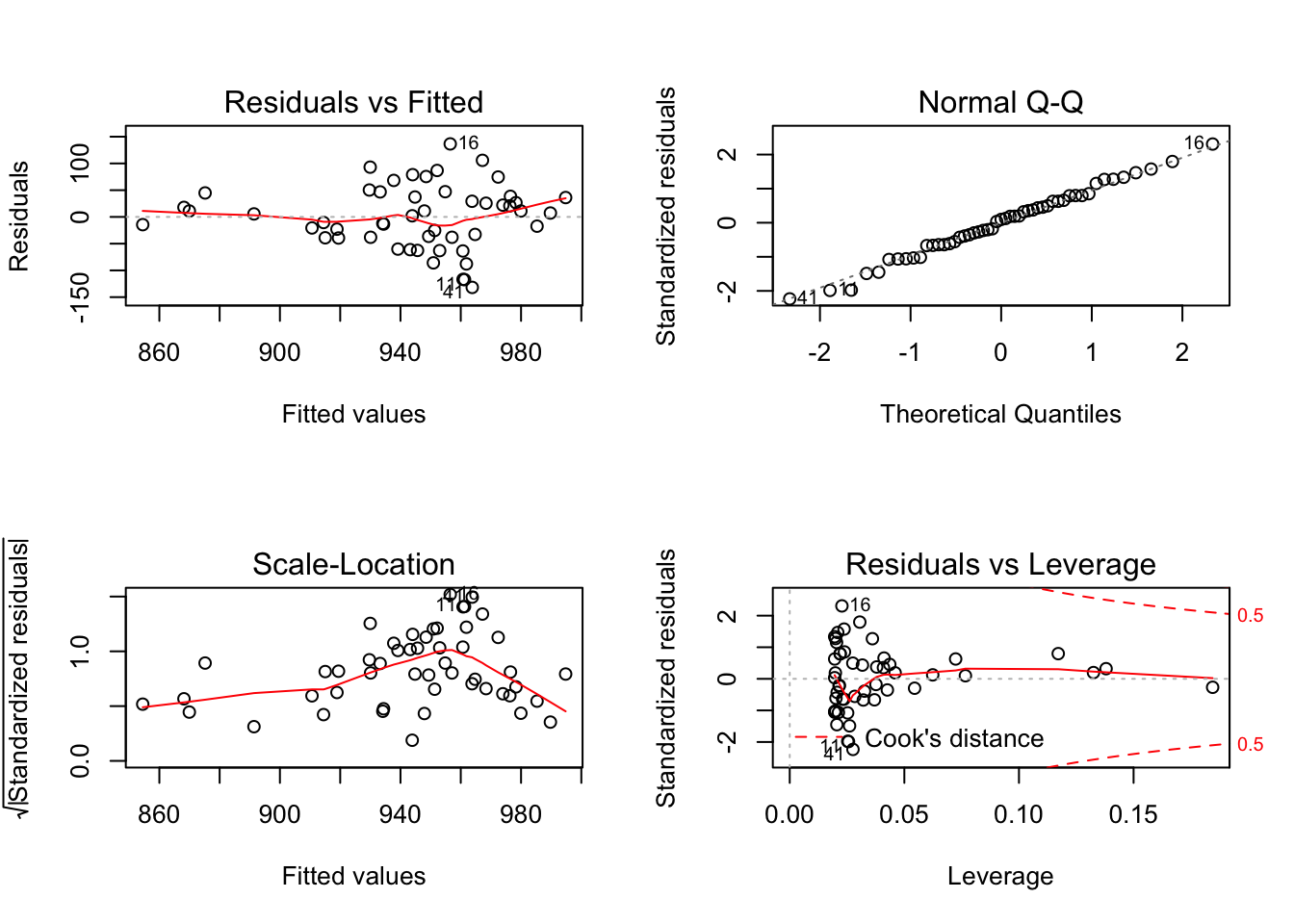
Comparing models
Do congressional voting patterns predict SAT scores over and above expense? Fit two models and compare them:
# fit another model, adding house and senate as predictors
sat_voting_mod <- lm(csat ~ 1 + expense + house + senate,
data = na.omit(states_data))
summary(sat_voting_mod) %>% coef()## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1082.9343804 38.63381274 28.030741 1.06779e-29
## expense -0.0187083 0.00969149 -1.930385 6.00200e-02
## house -1.4424375 0.60047838 -2.402147 2.05867e-02
## senate 0.4981786 0.51356136 0.970047 3.37326e-01Why are we using na.omit()? Let’s see what na.omit() does.
# fake data
dat <- data.frame(
x = 1:5,
y = c(3, 2, 1, NA, 5),
z = c(6, NA, 2, 7, 3))
dat## x y z
## 1 1 3 6
## 2 2 2 NA
## 3 3 1 2
## 4 4 NA 7
## 5 5 5 3na.omit(dat) # listwise deletion of observations## x y z
## 1 1 3 6
## 3 3 1 2
## 5 5 5 3# also see
# ?complete.cases
dat[with(dat, complete.cases(x, y, z)), ]## x y z
## 1 1 3 6
## 3 3 1 2
## 5 5 5 3To compare models, we must fit them to the same data. This is why we need na.omit(). Now let’s update our first model using na.omit():
sat_mod <-
sat_mod %>%
update(data = na.omit(states_data))
# compare using an F-test with the anova() function
anova(sat_mod, sat_voting_mod)## Analysis of Variance Table
##
## Model 1: csat ~ 1 + expense
## Model 2: csat ~ 1 + expense + house + senate
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 46 169050
## 2 44 149284 2 19766 2.913 0.0649Exercise 0
Ordinary least squares regression
Use the states.rds data set. Fit a model predicting energy consumed per capita (energy) from the percentage of residents living in metropolitan areas (metro). Be sure to
- Examine/plot the data before fitting the model
## - Print and interpret the model
summary()
## plot()the model to look for deviations from modeling assumptions
## - Select one or more additional predictors to add to your model and repeat steps 1-3. Is this model significantly better than the model with
metroas the only predictor?
## Click for Exercise 0 Solution
Use the states.rds data set.
states <- read_rds("dataSets/states.rds")Fit a model predicting energy consumed per capita (energy) from the percentage of residents living in metropolitan areas (metro). Be sure to:
- Examine/plot the data before fitting the model.
states_en_met <-
states %>%
select(metro, energy)
summary(states_en_met)## metro energy
## Min. : 20.4 Min. :200
## 1st Qu.: 47.0 1st Qu.:285
## Median : 67.5 Median :320
## Mean : 64.1 Mean :354
## 3rd Qu.: 81.6 3rd Qu.:372
## Max. :100.0 Max. :991
## NA's :1 NA's :1 plot(states_en_met)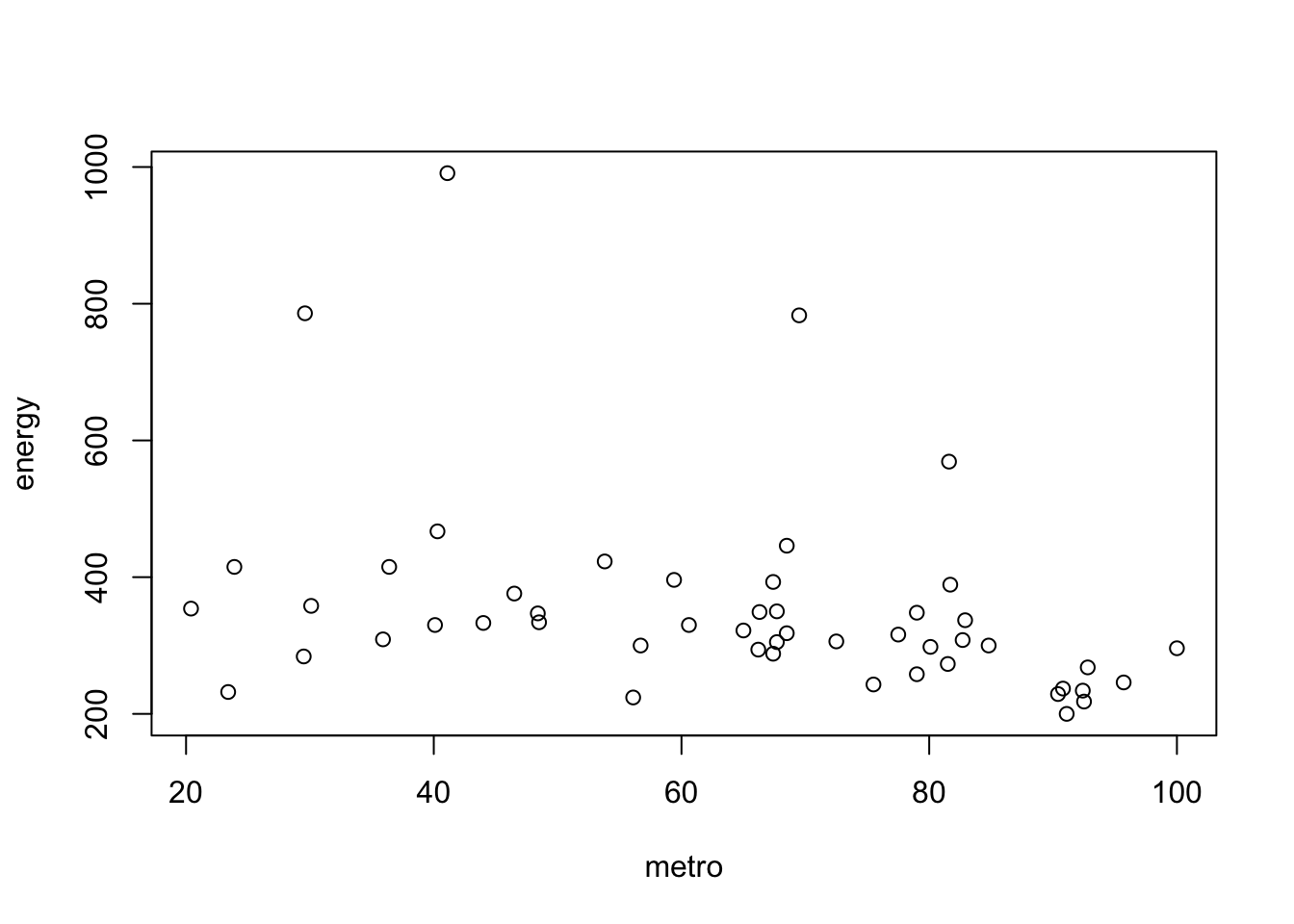
cor(states_en_met, use = "pairwise")## metro energy
## metro 1.000000 -0.339745
## energy -0.339745 1.000000- Print and interpret the model
summary().
mod_en_met <- lm(energy ~ metro, data = states)
summary(mod_en_met)##
## Call:
## lm(formula = energy ~ metro, data = states)
##
## Residuals:
## Min 1Q Median 3Q Max
## -215.5 -64.5 -30.9 18.7 584.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 501.029 61.814 8.11 0.00000000015
## metro -2.287 0.914 -2.50 0.016
##
## Residual standard error: 140 on 48 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.115, Adjusted R-squared: 0.097
## F-statistic: 6.26 on 1 and 48 DF, p-value: 0.0158plot()the model to look for deviations from modeling assumptions.
par(mfrow = c(2, 2)) # splits the plotting window into 4 panels
plot(mod_en_met)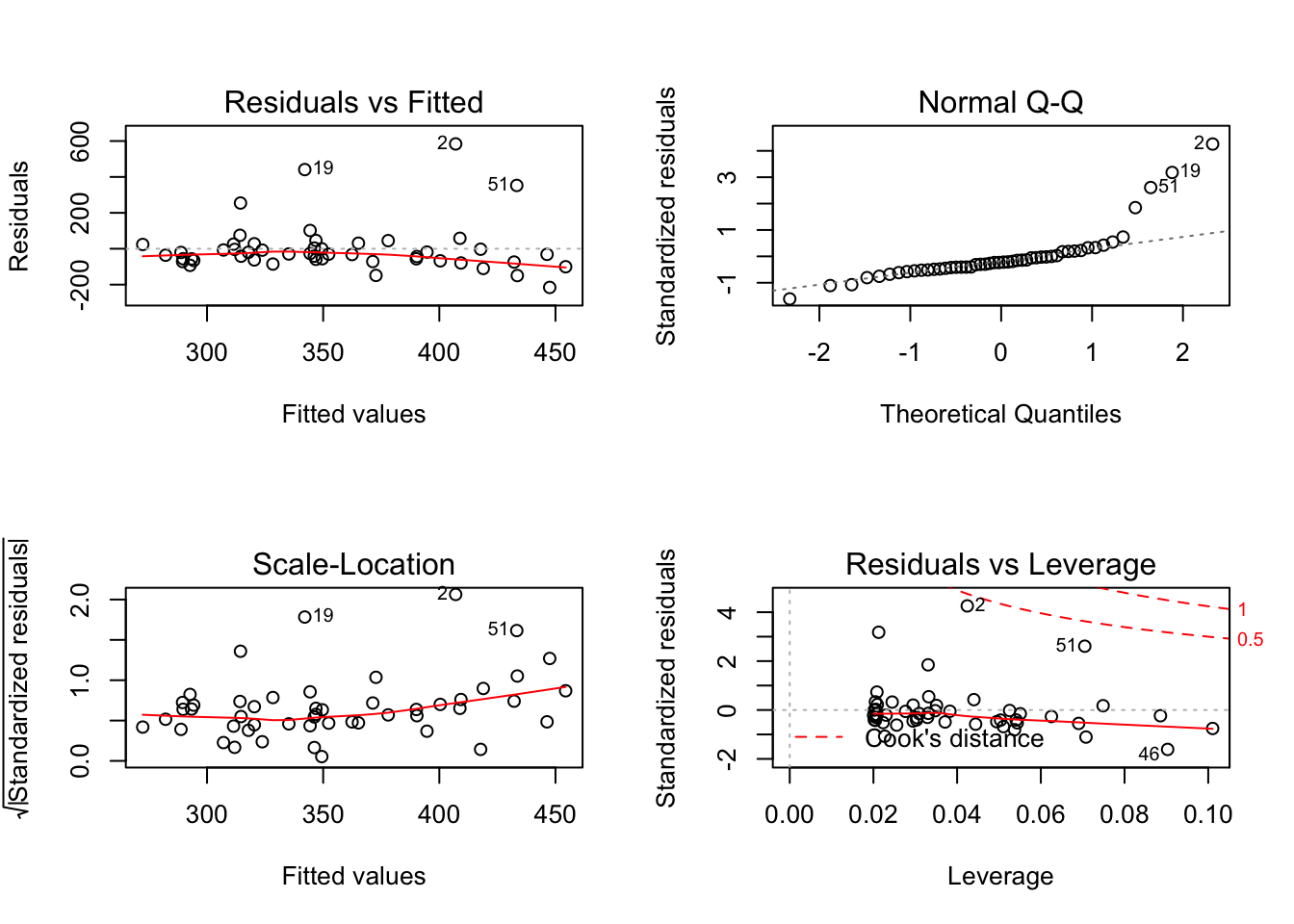
- Select one or more additional predictors to add to your model and repeat steps 1-3. Is this model significantly better than the model with metro as the only predictor?
states_en_met_pop_wst <-
states %>%
select(energy, metro, pop, waste)
summary(states_en_met_pop_wst)## energy metro pop waste
## Min. :200 Min. : 20.4 Min. : 454000 Min. :0.540
## 1st Qu.:285 1st Qu.: 47.0 1st Qu.: 1299750 1st Qu.:0.823
## Median :320 Median : 67.5 Median : 3390500 Median :0.960
## Mean :354 Mean : 64.1 Mean : 4962040 Mean :0.989
## 3rd Qu.:372 3rd Qu.: 81.6 3rd Qu.: 5898000 3rd Qu.:1.145
## Max. :991 Max. :100.0 Max. :29760000 Max. :1.510
## NA's :1 NA's :1 NA's :1 NA's :1 plot(states_en_met_pop_wst)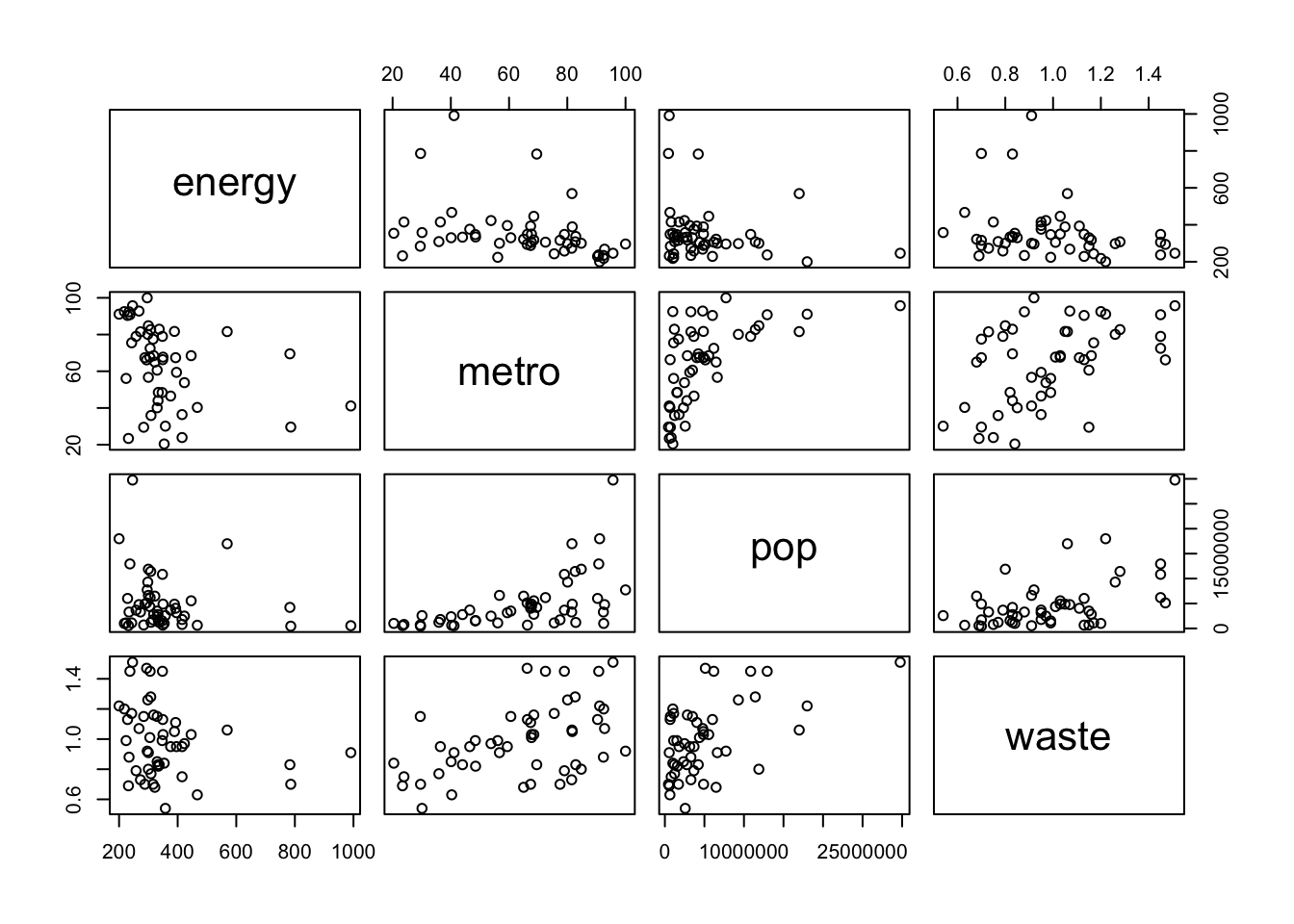
cor(states_en_met_pop_wst, use = "pairwise")## energy metro pop waste
## energy 1.000000 -0.339745 -0.184036 -0.252650
## metro -0.339745 1.000000 0.565356 0.487788
## pop -0.184036 0.565356 1.000000 0.525571
## waste -0.252650 0.487788 0.525571 1.000000 mod_en_met_pop_waste <- lm(energy ~ 1 + metro + pop + waste, data = states)
summary(mod_en_met_pop_waste)##
## Call:
## lm(formula = energy ~ 1 + metro + pop + waste, data = states)
##
## Residuals:
## Min 1Q Median 3Q Max
## -224.6 -67.5 -31.8 12.7 589.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 561.66773812 99.04681924 5.67 0.0000009
## metro -2.07914840 1.16786868 -1.78 0.082
## pop 0.00000165 0.00000481 0.34 0.733
## waste -83.07494970 104.21963267 -0.80 0.429
##
## Residual standard error: 142 on 46 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.128, Adjusted R-squared: 0.0707
## F-statistic: 2.24 on 3 and 46 DF, p-value: 0.096 anova(mod_en_met, mod_en_met_pop_waste)## Analysis of Variance Table
##
## Model 1: energy ~ metro
## Model 2: energy ~ 1 + metro + pop + waste
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 48 943103
## 2 46 930153 2 12949 0.32 0.728Interactions & factors
GOAL: To learn how to specify interaction effects and fit models with categorical predictors. In particular:
- Formula syntax for interaction effects
- Factor levels and labels
- Contrasts and pairwise comparisons
Modeling interactions
Interactions allow us assess the extent to which the association between one predictor and the outcome depends on a second predictor. For example: Does the association between expense and SAT scores depend on the median income in the state?
# Add the interaction to the model
sat_expense_by_percent <- lm(csat ~ 1 + expense + income + expense : income, data = states_data)
# same as above, but shorter syntax
sat_expense_by_percent <- lm(csat ~ 1 + expense * income, data = states_data)
# Show the regression coefficients table
summary(sat_expense_by_percent) %>% coef() ## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1380.36423333 172.086252477 8.02135 0.000000000236707
## expense -0.06384067 0.032700873 -1.95226 0.056878369245142
## income -10.49785114 4.991463374 -2.10316 0.040832525070882
## expense:income 0.00138465 0.000863553 1.60343 0.115539488252897Regression with categorical predictors
Let’s try to predict SAT scores from region, a categorical variable. Note that you must make sure R does not think your categorical variable is numeric.
# make sure R knows region is categorical
str(states_data$region)## Factor w/ 4 levels "West","N. East",..: 3 1 1 3 1 1 2 3 NA 3 ... states_data$region <- factor(states_data$region)
# arguments to the factor() function
# factor(x, levels, labels)
levels(states_data$region)## [1] "West" "N. East" "South" "Midwest" # Add region to the model
sat_region <- lm(csat ~ 1 + region, data = states_data)
# Show the results
summary(sat_region) %>% coef() # show the regression coefficients table## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 946.3077 14.7958 63.957781 1.35258e-46
## regionN. East -56.7521 23.1328 -2.453314 1.80038e-02
## regionSouth -16.3077 19.9195 -0.818681 4.17190e-01
## regionMidwest 63.7756 21.3559 2.986321 4.51415e-03 anova(sat_region) # show ANOVA table## Analysis of Variance Table
##
## Response: csat
## Df Sum Sq Mean Sq F value Pr(>F)
## region 3 82049 27350 9.61 0.0000486
## Residuals 46 130912 2846So, make sure to tell R which variables are categorical by converting them to factors!
Setting factor reference groups & contrasts
Contrasts is the umbrella term used to describe the process of testing linear combinations of parameters from regression models. All statistical sofware use contrasts, but each software has different defaults and their own way of overriding these.
The default contrasts in R are “treatment” contrasts (aka “dummy coding”), where each level within a factor is identified within a matrix of binary 0 / 1 variables, with the first level chosen as the reference category.They’re called “treatment” contrasts, because of the typical use case where there is one control group (the reference group) and one or more treatment groups that are to be compared to the controls. It is easy to change the default contrasts to something other than treatment contrasts, though this is rarely needed. More often, we may want to change the reference group in treatment contrasts or get all sets of pairwise contrasts between factor levels.
# default treatment (dummy) contrasts
contrasts(states_data$region)## N. East South Midwest
## West 0 0 0
## N. East 1 0 0
## South 0 1 0
## Midwest 0 0 1 # change the reference group
states_data$region <- relevel(states_data$region, ref = "Midwest")
# check the reference group has changed
contrasts(states_data$region)## West N. East South
## Midwest 0 0 0
## West 1 0 0
## N. East 0 1 0
## South 0 0 1 # refit the model
mod_region <- lm(csat ~ 1 + region, data = states_data)
summary(mod_region) %>% coef()## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1010.0833 15.4000 65.58993 4.29631e-47
## regionWest -63.7756 21.3559 -2.98632 4.51415e-03
## regionN. East -120.5278 23.5239 -5.12364 5.79840e-06
## regionSouth -80.0833 20.3723 -3.93100 2.82601e-04 # get all pairwise contrasts between means
mod_region %>%
emmeans(specs = pairwise ~ region)## $emmeans
## region emmean SE df lower.CL upper.CL
## Midwest 1010 15.4 46 979 1041
## West 946 14.8 46 917 976
## N. East 890 17.8 46 854 925
## South 930 13.3 46 903 957
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## Midwest - West 63.8 21.4 46 2.986 0.0226
## Midwest - N. East 120.5 23.5 46 5.124 <.0001
## Midwest - South 80.1 20.4 46 3.931 0.0016
## West - N. East 56.8 23.1 46 2.453 0.0812
## West - South 16.3 19.9 46 0.819 0.8453
## N. East - South -40.4 22.2 46 -1.820 0.2774
##
## P value adjustment: tukey method for comparing a family of 4 estimatesExercise 1
Interactions & factors
Use the states data set.
- Add on to the regression equation that you created in Exercise 1 by generating an interaction term and testing the interaction.
## - Try adding region to the model. Are there significant differences across the four regions?
## Click for Exercise 1 Solution
Use the states data set.
- Add on to the regression equation that you created in exercise 1 by generating an interaction term and testing the interaction.
mod_en_metro_by_waste <- lm(energy ~ 1 + metro * waste, data = states)- Try adding a region to the model. Are there significant differences across the four regions?
mod_en_region <- lm(energy ~ 1 + metro * waste + region, data = states)
anova(mod_en_metro_by_waste, mod_en_region)## Analysis of Variance Table
##
## Model 1: energy ~ 1 + metro * waste
## Model 2: energy ~ 1 + metro * waste + region
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 46 930683
## 2 43 821247 3 109436 1.91 0.142Models with binary outcomes
GOAL: To learn how to use the glm() function to model binary outcomes. In particular:
- The
familyandlinkcomponents of theglm()function call - Transforming model coefficients into odds ratios
- Transforming model coefficients into predicted marginal means
Logistic regression
This far we have used the lm() function to fit our regression models. lm() is great, but limited — in particular it only fits models for continuous dependent variables. For categorical dependent variables we can use the glm() function.
For these models we will use a different dataset, drawn from the National Health Interview Survey. From the CDC website:
The National Health Interview Survey (NHIS) has monitored the health of the nation since 1957. NHIS data on a broad range of health topics are collected through personal household interviews. For over 50 years, the U.S. Census Bureau has been the data collection agent for the National Health Interview Survey. Survey results have been instrumental in providing data to track health status, health care access, and progress toward achieving national health objectives.
Load the National Health Interview Survey data:
NH11 <- read_rds("dataSets/NatHealth2011.rds")Logistic regression example
Motivation for a logistic regression model — with a binary response:
- Errors will not be normally distributed
- Variance will not be homoskedastic
- Predictions should be constrained to be on the interval [0, 1]
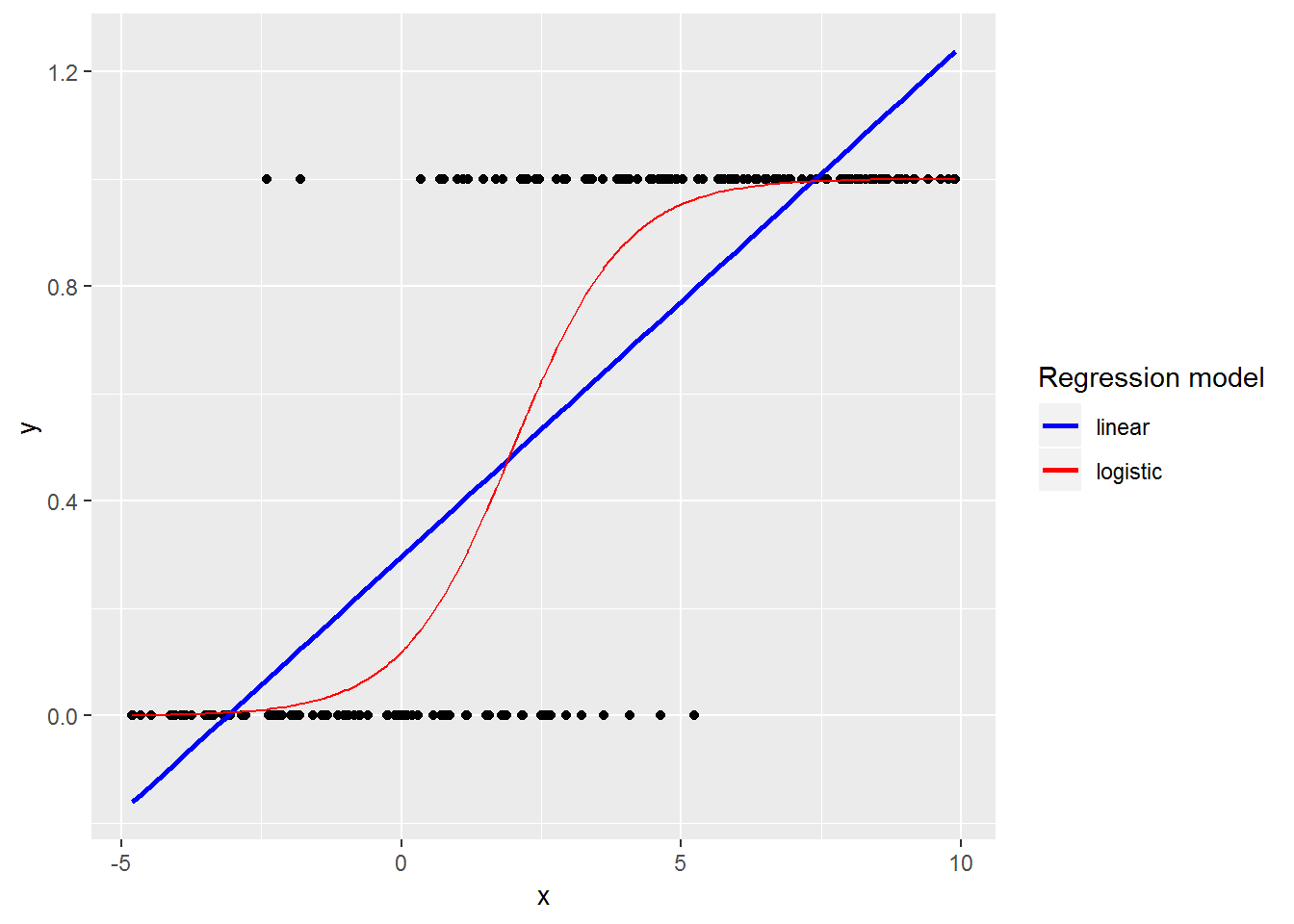
Anatomy of a generalized linear model:
# OLS model using lm()
lm(outcome ~ 1 + pred1 + pred2,
data = mydata)
# OLS model using glm()
glm(outcome ~ 1 + pred1 + pred2,
data = mydata,
family = gaussian(link = "identity"))
# logistic model using glm()
glm(outcome ~ 1 + pred1 + pred2,
data = mydata,
family = binomial(link = "logit"))The family argument sets the error distribution for the model, while the link function argument relates the predictors to the expected value of the outcome.
Let’s predict the probability of being diagnosed with hypertension based on age, sex, sleep, and bmi. Here’s the model:
\[ logit(hypev_i) = \beta_{0}1 + \beta_1agep_i + \beta_2sex_i + \beta_3sleep_i + \beta_4bmi_i + \epsilon_i \]
where \(logit(\cdot)\) is the link function, which is equivalent to the log odds of hypev:
\[ logit(hypev_i) = ln \frac{p(hypev_i = 1)}{p(hypev_i = 0)} \]
And here’s how we fit this in R. First, let’s clean up the hypertension outcome by making it binary:
str(NH11$hypev) # check stucture of hypev## Factor w/ 5 levels "1 Yes","2 No",..: 2 2 1 2 2 1 2 2 1 2 ... levels(NH11$hypev) # check levels of hypev## [1] "1 Yes" "2 No" "7 Refused" "8 Not ascertained" "9 Don't know" # collapse all missing values to NA
NH11$hypev <- factor(NH11$hypev, levels=c("2 No", "1 Yes"))Now let’s use glm() to estimate the model:
# run our regression model
hyp_out <- glm(hypev ~ 1 + age_p + sex + sleep + bmi,
data = NH11,
family = binomial(link = "logit"))
summary(hyp_out) %>% coef()## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.26946603 0.056494729 -75.57282 0.00000e+00
## age_p 0.06069930 0.000822721 73.77874 0.00000e+00
## sex2 Female -0.14402509 0.026797660 -5.37454 7.67785e-08
## sleep -0.00703578 0.001639720 -4.29084 1.77998e-05
## bmi 0.01857170 0.000951083 19.52691 6.48517e-85Odds ratios
Generalized linear models use link functions to relate the average value of the response to the predictors, so raw coefficients are difficult to interpret. For example, the age coefficient of .06 in the previous model tells us that for every one unit increase in age, the log odds of hypertension diagnosis increases by 0.06. Since most of us are not used to thinking in log odds this is not too helpful!
One solution is to transform the coefficients to make them easier to interpret. Here we transform them into odds ratios by exponentiating:
# point estimates
coef(hyp_out) %>% exp()## (Intercept) age_p sex2 Female sleep bmi
## 0.0139893 1.0625794 0.8658660 0.9929889 1.0187452 # confidence intervals
confint(hyp_out) %>% exp()## 2.5 % 97.5 %
## (Intercept) 0.0125168 0.0156197
## age_p 1.0608738 1.0643008
## sex2 Female 0.8215520 0.9125501
## sleep 0.9897876 0.9961747
## bmi 1.0168514 1.0206501Predicted marginal means
Instead of reporting odds ratios, we may want to calculate predicted marginal means (sometimes called “least squares means”). These are average values of the outcome at particular levels of the predictors. For ease of interpretation, we want these marginal means to be on the response scale (i.e., the probability scale). We can use the effects package to compute these quantities of interest for us (by default, the numerical output will be on the response scale).
hyp_out %>%
allEffects() %>%
plot(type = "response") # "response" refers to the probability scale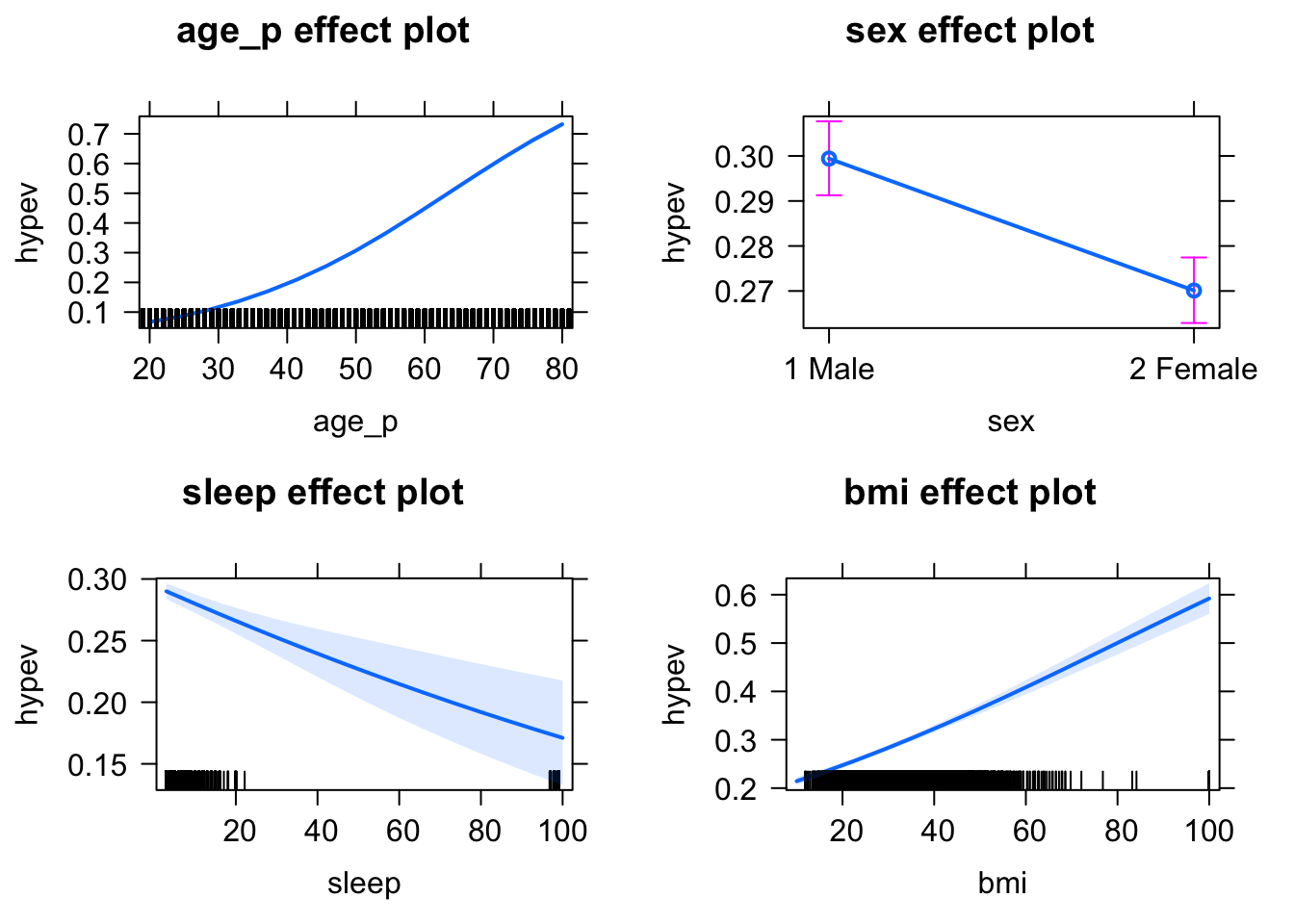
# generate a sequence of ages at which to get predictions of the outcome
age_years <- seq(20, 80, by = 5)
age_years## [1] 20 25 30 35 40 45 50 55 60 65 70 75 80 eff_df <-
hyp_out %>%
allEffects(xlevels = list(age_p = age_years)) %>% # override defaults for age
as.data.frame() # get confidence intervals
eff_df## $age_p
## age_p fit se lower upper
## 1 20 0.0669038 0.00191570 0.0632455 0.0707578
## 2 25 0.0885269 0.00218162 0.0843432 0.0928971
## 3 30 0.1162677 0.00241881 0.1116102 0.1210931
## 4 35 0.1512588 0.00260324 0.1462269 0.1564320
## 5 40 0.1944632 0.00272243 0.1891828 0.1998547
## 6 45 0.2464253 0.00279626 0.2409858 0.2519468
## 7 50 0.3069807 0.00289586 0.3013344 0.3126855
## 8 55 0.3750116 0.00312411 0.3689087 0.3811544
## 9 60 0.4483648 0.00353179 0.4414530 0.4552965
## 10 65 0.5240356 0.00405245 0.5160876 0.5319716
## 11 70 0.5986188 0.00454553 0.5896780 0.6074944
## 12 75 0.6688990 0.00488073 0.6592642 0.6783943
## 13 80 0.7323751 0.00498654 0.7224891 0.7420346
##
## $sex
## sex fit se lower upper
## 1 1 Male 0.299419 0.00418871 0.291274 0.307692
## 2 2 Female 0.270104 0.00371503 0.262885 0.277447
##
## $sleep
## sleep fit se lower upper
## 1 3 0.289994 0.00327643 0.283615 0.296458
## 2 30 0.252489 0.00742700 0.238212 0.267322
## 3 50 0.226866 0.01244618 0.203401 0.252181
## 4 80 0.191984 0.01854946 0.158220 0.230977
## 5 100 0.171095 0.02158429 0.132829 0.217620
##
## $bmi
## bmi fit se lower upper
## 1 10 0.214408 0.00412159 0.206441 0.222597
## 2 30 0.283509 0.00284941 0.277958 0.289127
## 3 60 0.408549 0.00745016 0.394031 0.423227
## 4 80 0.500366 0.01213914 0.476591 0.524140
## 5 100 0.592159 0.01618007 0.560105 0.623448Exercise 2
Logistic regression
Use the NH11 data set that we loaded earlier.
- Use
glm()to conduct a logistic regression to predict ever worked (everwrk) using age (age_p) and marital status (r_maritl). Make sure you only keep the following two levels foreverwrk(1 Yesand2 No). Hint: use thefactor()function. Also, make sure to drop anyr_maritllevels that do not contain observations. Hint: see?droplevels.
## - Predict the probability of working for each level of marital status. Hint: use
allEffects()
## Note that the data are not perfectly clean and ready to be modeled. You will need to clean up at least some of the variables before fitting the model.
Click for Exercise 2 Solution
Use the NH11 data set that we loaded earlier. Note that the data is not perfectly clean and ready to be modeled. You will need to clean up at least some of the variables before fitting the model.
- Use
glm()to conduct a logistic regression to predict ever worked (everwrk) using age (age_p) and marital status (r_maritl). Make sure you only keep the following two levels foreverwrk(1 Yesand2 No). Hint: use thefactor()function. Also, make sure to drop anyr_maritllevels that do not contain observations. Hint: see?droplevels.
NH11 <-
NH11 %>%
mutate(everwrk = factor(everwrk, levels = c("1 Yes", "2 No")),
r_maritl = droplevels(r_maritl)
)
mod_wk_age_mar <- glm(everwrk ~ 1 + age_p + r_maritl,
data = NH11,
family = binomial(link = "logit"))
summary(mod_wk_age_mar)##
## Call:
## glm(formula = everwrk ~ 1 + age_p + r_maritl, family = binomial(link = "logit"),
## data = NH11)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.044 -0.565 -0.439 -0.337 2.731
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.44025 0.09354 -4.71 0.00000251841905292
## age_p -0.02981 0.00165 -18.12 < 2e-16
## r_maritl2 Married - spouse not in household 0.04968 0.21731 0.23 0.8192
## r_maritl4 Widowed 0.68362 0.08434 8.11 0.00000000000000052
## r_maritl5 Divorced -0.73011 0.11168 -6.54 0.00000000006254929
## r_maritl6 Separated -0.12809 0.15137 -0.85 0.3974
## r_maritl7 Never married 0.34361 0.06922 4.96 0.00000069100229497
## r_maritl8 Living with partner -0.44358 0.13777 -3.22 0.0013
## r_maritl9 Unknown marital status 0.39548 0.49297 0.80 0.4224
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 11082 on 14039 degrees of freedom
## Residual deviance: 10309 on 14031 degrees of freedom
## (18974 observations deleted due to missingness)
## AIC: 10327
##
## Number of Fisher Scoring iterations: 5- Predict the probability of working for each level of marital status. Hint: use
allEffects().
mod_wk_age_mar %>%
allEffects() %>%
as.data.frame()## $age_p
## age_p fit se lower upper
## 1 20 0.2758744 0.01144854 0.2540091 0.2988678
## 2 30 0.2204336 0.00748365 0.2061163 0.2354505
## 3 50 0.1347747 0.00318375 0.1286557 0.1411376
## 4 70 0.0790279 0.00305362 0.0732463 0.0852239
## 5 80 0.0598752 0.00312393 0.0540376 0.0662991
##
## $r_maritl
## r_maritl fit se lower upper
## 1 1 Married - spouse in household 0.1082200 0.00425964 0.1001498 0.1168561
## 2 2 Married - spouse not in household 0.1131082 0.02139317 0.0774606 0.1622753
## 3 4 Widowed 0.1938109 0.01063476 0.1738136 0.2155087
## 4 5 Divorced 0.0552439 0.00536166 0.0456288 0.0667436
## 5 6 Separated 0.0964642 0.01270750 0.0742682 0.1244022
## 6 7 Never married 0.1461100 0.00745921 0.1320878 0.1613441
## 7 8 Living with partner 0.0722496 0.00890495 0.0566247 0.0917666
## 8 9 Unknown marital status 0.1527008 0.06352845 0.0644084 0.3205573Multilevel modeling
GOAL: To learn about how to use the lmer() function to model clustered data. In particular:
- The formula syntax for incorporating random effects into a model
- Calculating the intraclass correlation (ICC)
- Model comparison for fixed and random effects
Multilevel modeling overview
- Multi-level (AKA hierarchical) models are a type of mixed-effects model
- They are used to model data that are clustered (i.e., non-independent)
- Mixed-effecs models include two types of predictors: fixed-effects and random effects
- Fixed-effects – observed levels are of direct interest (.e.g, sex, political party…)
- Random-effects – observed levels not of direct interest: goal is to make inferences to a population represented by observed levels
- In R, the
lme4package is the most popular for mixed effects models - Use the
lmer()function for liner mixed models,glmer()for generalized linear mixed models
The Exam data
The Exam data set contans exam scores of 4,059 students from 65 schools in Inner London. The variable names are as follows:
| Variable | Description |
|---|---|
| school | School ID - a factor. |
| normexam | Normalized exam score. |
| standLRT | Standardised LR test score. |
| student | Student id (within school) - a factor |
Exam <- read_rds("dataSets/Exam.rds")The null model & ICC
As a preliminary step it is often useful to partition the variance in the dependent variable into the various levels. This can be accomplished by running a null model (i.e., a model with a random effects grouping structure, but no fixed-effects predictors).
# anatomy of lmer() function
lmer(outcome ~ 1 + pred1 + pred2 + (1 | grouping_variable),
data = mydata) # null model, grouping by school but not fixed effects.
Norm1 <-lmer(normexam ~ 1 + (1 | school),
data = na.omit(Exam))
summary(Norm1)## Linear mixed model fit by REML ['lmerMod']
## Formula: normexam ~ 1 + (1 | school)
## Data: na.omit(Exam)
##
## REML criterion at convergence: 9962.9
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.875 -0.645 0.004 0.689 3.684
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 0.163 0.404
## Residual 0.852 0.923
## Number of obs: 3662, groups: school, 65
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.0131 0.0531 -0.25The is .161/(.161 + .852) = .159 = 16% of the variance is at the school level.
There is no consensus on how to calculate p-values for MLMs; hence why they are omitted from the lme4 output. But, if you really need p-values, the lmerTest package will calculate p-values for you (using the Satterthwaite approximation).
Adding fixed-effects predictors
Here’s a model that predicts exam scores from student’s standardized tests scores:
\[ normexam_{ij} = \mu1 + \beta_1standLRT_{ij} + U_{0j} + \epsilon_{ij} \]
where \(U_{0j}\) is the random intercept for the \(j\)th school. Let’s implement this in R using lmer():
Norm2 <-lmer(normexam ~ 1 + standLRT + (1 | school),
data = na.omit(Exam))
summary(Norm2) ## Linear mixed model fit by REML ['lmerMod']
## Formula: normexam ~ 1 + standLRT + (1 | school)
## Data: na.omit(Exam)
##
## REML criterion at convergence: 8483.5
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.673 -0.630 0.023 0.678 3.334
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 0.0937 0.306
## Residual 0.5692 0.754
## Number of obs: 3662, groups: school, 65
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.0000431 0.0405496 0.0
## standLRT 0.5669188 0.0132394 42.8
##
## Correlation of Fixed Effects:
## (Intr)
## standLRT 0.007Multiple degree of freedom comparisons
As with lm() and glm() models, you can compare the two lmer() models using the anova() function. With mixed effects models, this will produce a likelihood ratio test.
anova(Norm1, Norm2)## Data: na.omit(Exam)
## Models:
## Norm1: normexam ~ 1 + (1 | school)
## Norm2: normexam ~ 1 + standLRT + (1 | school)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## Norm1 3 9965 9984 -4979 9959
## Norm2 4 8480 8505 -4236 8472 1487 1 <2e-16Random slopes
Add a random effect of students’ standardized test scores as well. Now in addition to estimating the distribution of intercepts across schools, we also estimate the distribution of the slope of exam on standardized test.
Norm3 <- lmer(normexam ~ 1 + standLRT + (1 + standLRT | school),
data = na.omit(Exam))
summary(Norm3) ## Linear mixed model fit by REML ['lmerMod']
## Formula: normexam ~ 1 + standLRT + (1 + standLRT | school)
## Data: na.omit(Exam)
##
## REML criterion at convergence: 8442.8
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.790 -0.625 0.024 0.673 3.438
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 0.0909 0.302
## standLRT 0.0164 0.128 0.49
## Residual 0.5559 0.746
## Number of obs: 3662, groups: school, 65
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.0125 0.0401 -0.31
## standLRT 0.5609 0.0212 26.47
##
## Correlation of Fixed Effects:
## (Intr)
## standLRT 0.360Test the significance of the random slope
To test the significance of a random slope just compare models with and without the random slope term using a likelihood ratio test:
anova(Norm2, Norm3) ## Data: na.omit(Exam)
## Models:
## Norm2: normexam ~ 1 + standLRT + (1 | school)
## Norm3: normexam ~ 1 + standLRT + (1 + standLRT | school)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## Norm2 4 8480 8505 -4236 8472
## Norm3 6 8444 8481 -4216 8432 40.01 2 0.00000000205Exercise 3
Multilevel modeling
Use the bh1996 dataset:
## install.packages("multilevel")
data(bh1996, package="multilevel")From the data documentation:
Variables are Leadership Climate (
LEAD), Well-Being (WBEING), and Work Hours (HRS). The group identifier is namedGRP.
- Create a null model predicting wellbeing (
WBEING)
## - Calculate the ICC for your null model
## - Run a second multi-level model that adds two individual-level predictors, average number of hours worked (
HRS) and leadership skills (LEAD) to the model and interpret your output.
## - Now, add a random effect of average number of hours worked (
HRS) to the model and interpret your output. Test the significance of this random term.
## Click for Exercise 3 Solution
Use the dataset, bh1996:
# install.packages("multilevel")
data(bh1996, package="multilevel")From the data documentation:
Variables are Leadership Climate (
LEAD), Well-Being (WBEING), and Work Hours (HRS). The group identifier is namedGRP.
- Create a null model predicting wellbeing (
WBEING).
mod_grp0 <- lmer(WBEING ~ 1 + (1 | GRP), data = na.omit(bh1996))
summary(mod_grp0)## Linear mixed model fit by REML ['lmerMod']
## Formula: WBEING ~ 1 + (1 | GRP)
## Data: na.omit(bh1996)
##
## REML criterion at convergence: 19347.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.322 -0.648 0.031 0.718 2.667
##
## Random effects:
## Groups Name Variance Std.Dev.
## GRP (Intercept) 0.0358 0.189
## Residual 0.7895 0.889
## Number of obs: 7382, groups: GRP, 99
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 2.7743 0.0222 125- Run a second multi-level model that adds two individual-level predictors, average number of hours worked (
HRS) and leadership skills (LEAD) to the model and interpret your output.
mod_grp1 <- lmer(WBEING ~ 1 + HRS + LEAD + (1 | GRP), data = na.omit(bh1996))
summary(mod_grp1)## Linear mixed model fit by REML ['lmerMod']
## Formula: WBEING ~ 1 + HRS + LEAD + (1 | GRP)
## Data: na.omit(bh1996)
##
## REML criterion at convergence: 17860
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.919 -0.659 0.038 0.704 3.644
##
## Random effects:
## Groups Name Variance Std.Dev.
## GRP (Intercept) 0.0193 0.139
## Residual 0.6467 0.804
## Number of obs: 7382, groups: GRP, 99
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 1.68616 0.06770 24.91
## HRS -0.03162 0.00438 -7.22
## LEAD 0.50074 0.01281 39.09
##
## Correlation of Fixed Effects:
## (Intr) HRS
## HRS -0.800
## LEAD -0.635 0.121- Now, add a random effect of average number of hours worked (
HRS) to the model and interpret your output. Test the significance of this random term.
mod_grp2 <- lmer(WBEING ~ 1 + HRS + LEAD + (1 + HRS | GRP), data = na.omit(bh1996))
anova(mod_grp1, mod_grp2)## Data: na.omit(bh1996)
## Models:
## mod_grp1: WBEING ~ 1 + HRS + LEAD + (1 | GRP)
## mod_grp2: WBEING ~ 1 + HRS + LEAD + (1 + HRS | GRP)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## mod_grp1 5 17848 17882 -8919 17838
## mod_grp2 7 17851 17899 -8918 17837 1.22 2 0.543Wrap-up
Feedback
These workshops are a work in progress, please provide any feedback to: help@iq.harvard.edu
Resources
- IQSS
- Workshops: https://dss.iq.harvard.edu/workshop-materials
- Data Science Services: https://dss.iq.harvard.edu/
- Research Computing Environment: https://iqss.github.io/dss-rce/
- HBS
- Research Computing Services workshops: https://training.rcs.hbs.org/workshops
- Other HBS RCS resources: https://training.rcs.hbs.org/workshop-materials
- RCS consulting email: mailto:research@hbs.edu